


Next: Un punto materiale, di
Up: Lo studente svolga i
Previous: Lo studente svolga i
Sia
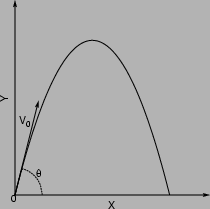
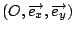 il sistema di assi cartesiani rappresentato in figura.
il sistema di assi cartesiani rappresentato in figura.
In questo sistema di assi,
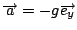 .
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova:
.
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova:
Dalla prima relazione si ottiene 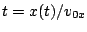 . Sostituendo nella
seconda, si ottiene l'equazione della traiettoria:
. Sostituendo nella
seconda, si ottiene l'equazione della traiettoria:
La gittata 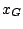 si ottiene risolvendo
si ottiene risolvendo 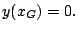 Otteniamo:
Otteniamo:
equazione che ammette due soluzioni: 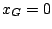 (che corrisponde al
punto di partenza) e
(che corrisponde al
punto di partenza) e
che è il valore della gittata. Notando che
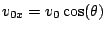 e
e
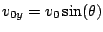 si ricava l'espressione di
si ricava l'espressione di 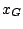 in funzione del modulo
in funzione del modulo 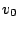 della velocità iniziale e dell'angolo
iniziale:
della velocità iniziale e dell'angolo
iniziale:
Il massimo di questa funzione si ottiene per
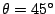 .
In quel caso
.
In quel caso
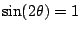 e
e
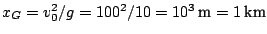 .
Non si può colpire un bersaglio posto ad una distanza
.
Non si può colpire un bersaglio posto ad una distanza 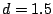 km
perchè è superiore a questa gittata massima (1 km).
km
perchè è superiore a questa gittata massima (1 km).



Next: Un punto materiale, di
Up: Lo studente svolga i
Previous: Lo studente svolga i
Nicolas Decamp
2005-11-22
![]() il sistema di assi cartesiani rappresentato in figura.
il sistema di assi cartesiani rappresentato in figura.
![]() .
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova:
.
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova: