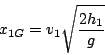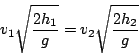Next: Un punto materiale di
Up: Lo studente svolga i
Previous: Lo studente svolga i
Sia
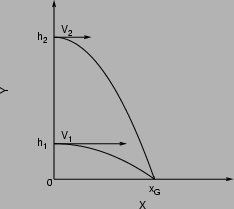
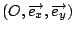 il sistema di assi cartesiani rappresentato in figura.
il sistema di assi cartesiani rappresentato in figura.
In questo sistema di assi,
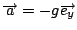 .
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova:
.
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova:
Dalla prima relazione si ottiene
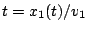 . Sostituendo
nella seconda, si ottiene l'equazione della traiettoria:
. Sostituendo
nella seconda, si ottiene l'equazione della traiettoria:
La gittata 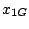 si ottiene risolvendo
si ottiene risolvendo
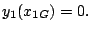 Otteniamo:
Otteniamo:
Una relazione equivalente si può scrivere per il secondo punto materiale.
Siccome 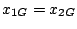 , si ottiene
, si ottiene
e dunque



Next: Un punto materiale di
Up: Lo studente svolga i
Previous: Lo studente svolga i
Nicolas Decamp
2005-11-22
![]() il sistema di assi cartesiani rappresentato in figura.
il sistema di assi cartesiani rappresentato in figura.
![]() .
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova:
.
Facendo una doppia integrazione rispetto al tempo e usando le condizioni
iniziali si trova: