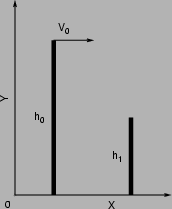
Dalla seconda legge di Newton si ottiene che il proiettile è sottoposto
ad un'accelerazione
![]() .
.
Effetuando una doppia integrazione rispetto al tempo ed usando le
condizioni iniziali si trova:
Il tempo ![]() in cui il proiettile supera il secondo muro si trova
scrivendo che
in cui il proiettile supera il secondo muro si trova
scrivendo che
![]() e vale:
e vale:
Questo valore si può sostituire nell'equazione per ![]() :
:
Se vogliamo che il proiettile superi il muro, ![]() deve essere
maggiore di
deve essere
maggiore di ![]() :
:
e dunque:
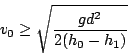
La velocità iniziale ![]() deve dunque essere maggiore di un valore
deve dunque essere maggiore di un valore
![]() , con:
, con:
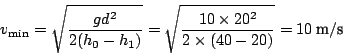
In questo caso: