


Next: Una massa (1 kg) legata
Up: Lo studente risolva i
Previous: Lo studente risolva i
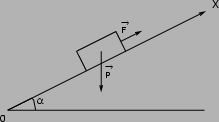
La macchina è sottoposta a due forze.
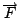 generata
dal motore, che la spinge verso l'alto e
generata
dal motore, che la spinge verso l'alto e
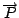 , la
forza peso. La seconda legge di Newton si scrive:
, la
forza peso. La seconda legge di Newton si scrive:
Proiettando lungo l'asse X (lungo il piano inclinato) si ottiene
Moltiplicando questa relazione per la velocità 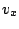 , si ottiene
, si ottiene
La potenza 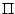 della macchina è il termine
della macchina è il termine 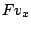 . Quando la
velocità è massima, l'accelerazione è nulla e abbiamo:
. Quando la
velocità è massima, l'accelerazione è nulla e abbiamo:
cioé:



Next: Una massa (1 kg) legata
Up: Lo studente risolva i
Previous: Lo studente risolva i
Nicolas Decamp
2005-11-22
![]() generata
dal motore, che la spinge verso l'alto e
generata
dal motore, che la spinge verso l'alto e
![]() , la
forza peso. La seconda legge di Newton si scrive:
, la
forza peso. La seconda legge di Newton si scrive:
![]() , si ottiene
, si ottiene