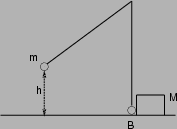
Scrivendo il teorema delle forze vive si trova l'espressione della
velocità ![]() di
di ![]() giusto prima dell'urto:
giusto prima dell'urto:
Essendo
![]() ad ogni istante perpendicolare allo
spostamento,
ad ogni istante perpendicolare allo
spostamento,
![]() . Il lavoro della forza peso
vale
. Il lavoro della forza peso
vale ![]() . La variazione di energia cinetica si scrive:
. La variazione di energia cinetica si scrive:
Dopo l'urto completamente anelastico, ![]() e
e ![]() proseguono unite.
La legge di conservazione della quantità di moto si scrive:
proseguono unite.
La legge di conservazione della quantità di moto si scrive:
e dunque: