


Next: Due pendoli semplici di
Up: Lo studente svolga i
Previous: Lo studente svolga i
Chiamiamo
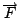 la forza esercitata dal sedile sul
pilota,
la forza esercitata dal sedile sul
pilota,
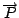 la forza peso del pilota e scriviamo
la seconda legge di Newton applicata al pilota:
la forza peso del pilota e scriviamo
la seconda legge di Newton applicata al pilota:
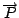 è verticale verso il basso, di modulo
è verticale verso il basso, di modulo 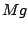 .
L'accelerazione
.
L'accelerazione
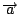 del pilota è quella dell'aereo.
Siccome il moto è circolare uniforme, l'accelerazione tangenziale
è nulla e
del pilota è quella dell'aereo.
Siccome il moto è circolare uniforme, l'accelerazione tangenziale
è nulla e 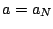 (accelerazione centripeta). Nel punto più basso
della traiettoria,
(accelerazione centripeta). Nel punto più basso
della traiettoria,
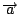 è verticale verso l'alto (perchè
in direzione del centro della traiettoria circolare) e di modulo
è verticale verso l'alto (perchè
in direzione del centro della traiettoria circolare) e di modulo 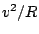 dove
dove 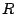 è il raggio della traiettoria circolare. Proiettando l'equazione
lungo un asse verticale diretto verso l'alto (Oz), si ottiene:
è il raggio della traiettoria circolare. Proiettando l'equazione
lungo un asse verticale diretto verso l'alto (Oz), si ottiene:
dunque
e, in unità del peso del pilota



Next: Due pendoli semplici di
Up: Lo studente svolga i
Previous: Lo studente svolga i
Nicolas Decamp
2005-11-22
![]() la forza esercitata dal sedile sul
pilota,
la forza esercitata dal sedile sul
pilota,
![]() la forza peso del pilota e scriviamo
la seconda legge di Newton applicata al pilota:
la forza peso del pilota e scriviamo
la seconda legge di Newton applicata al pilota: