


Next: Prova dell'11 dicembre 2000
Up: Lo studente svolga i
Previous: Un aereo compie a
Sia
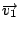 la velocità della massa
la velocità della massa 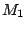 giusto
prima dell'urto, e siano
giusto
prima dell'urto, e siano
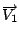 e
e
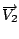 le velocità rispettive delle masse
le velocità rispettive delle masse 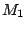 ed
ed 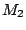 giusto dopo
l'urto.
giusto dopo
l'urto.
Dalla conservazione dell'energia meccanica durante il moto della massa
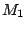 , immediatamente prima dell'urto, si puo scrivere che
, immediatamente prima dell'urto, si puo scrivere che
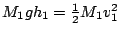 e dunque
e dunque
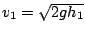 . Facendo lo stesso ragionamento per
il moto di
. Facendo lo stesso ragionamento per
il moto di 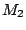 dopo l'urto, si ottiene
dopo l'urto, si ottiene
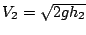 e dunque
e dunque
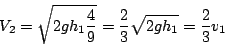 |
(1) |
Durante l'urto, la quantità di moto si conserva:
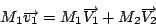 |
(2) |
Siccome l'urto è elastico centrale, l'energia cinetica di traslazione
è anche conservata:
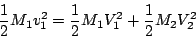 |
(3) |
Chiamiamo 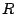 il rapporto tra le masse,
il rapporto tra le masse, 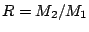 . L'equazione
(2) si può riscrivere
. L'equazione
(2) si può riscrivere
(con 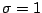 se
se
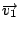 e
e
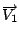 hanno lo stesso verso e
hanno lo stesso verso e 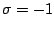 se hanno versi opposti). L'equazione
(3) si riscrive
se hanno versi opposti). L'equazione
(3) si riscrive
Usando l'equazione (1) si ottiene, per l'eq. (2)
che
e, per l'eq. (3):
Dalla (2) si ricava:
e dunque
che possiamo sostituire nell'eq. (3):
da cui si ottiene:



Next: Prova dell'11 dicembre 2000
Up: Lo studente svolga i
Previous: Un aereo compie a
Nicolas Decamp
2005-11-22
![]() la velocità della massa
la velocità della massa ![]() giusto
prima dell'urto, e siano
giusto
prima dell'urto, e siano
![]() e
e
![]() le velocità rispettive delle masse
le velocità rispettive delle masse ![]() ed
ed ![]() giusto dopo
l'urto.
giusto dopo
l'urto.
![]() , immediatamente prima dell'urto, si puo scrivere che
, immediatamente prima dell'urto, si puo scrivere che
![]() e dunque
e dunque
![]() . Facendo lo stesso ragionamento per
il moto di
. Facendo lo stesso ragionamento per
il moto di ![]() dopo l'urto, si ottiene
dopo l'urto, si ottiene
![]() e dunque
e dunque